1.4. Passing Input Parameters to Functions#

As we have seen in the previous section, we discussed the default method of passing input parameters to functions: pass-by-value, where the value of the input parameter is passed to the function. In this section, we will discuss the problems with pass-by-value and introduce two alternative methods: pass-by-pointer and pass-by-reference.

1.4.1. Problem with Pass-By-Value#

The main issue with pass-by-value is that its not always applicable to all cases. For example, if we were to write a function that takes in as input two variables and swaps their values, we would not be able to do so using pass-by-value.

For example, the following code snippet attempts to swap the values of two variables a and b using pass-by-value but fails to do so as the value of a and b in the main function remains unchanged.

Code


#include <iostream>
using namespace std;


void swapByValue(int a, int b);


int main(void) {
  int a = 5, b = 10;
  cout << "Before swapping: " << "a = " << a << ", b = " << b << endl;
  swapByValue(a, b);
  cout << "After swapping: " << "a = " << a << ", b = " << b << endl;
  return 0;
}


void swapByValue(int a, int b) {
  int temp = a;
  a = b;
  b = temp;
}

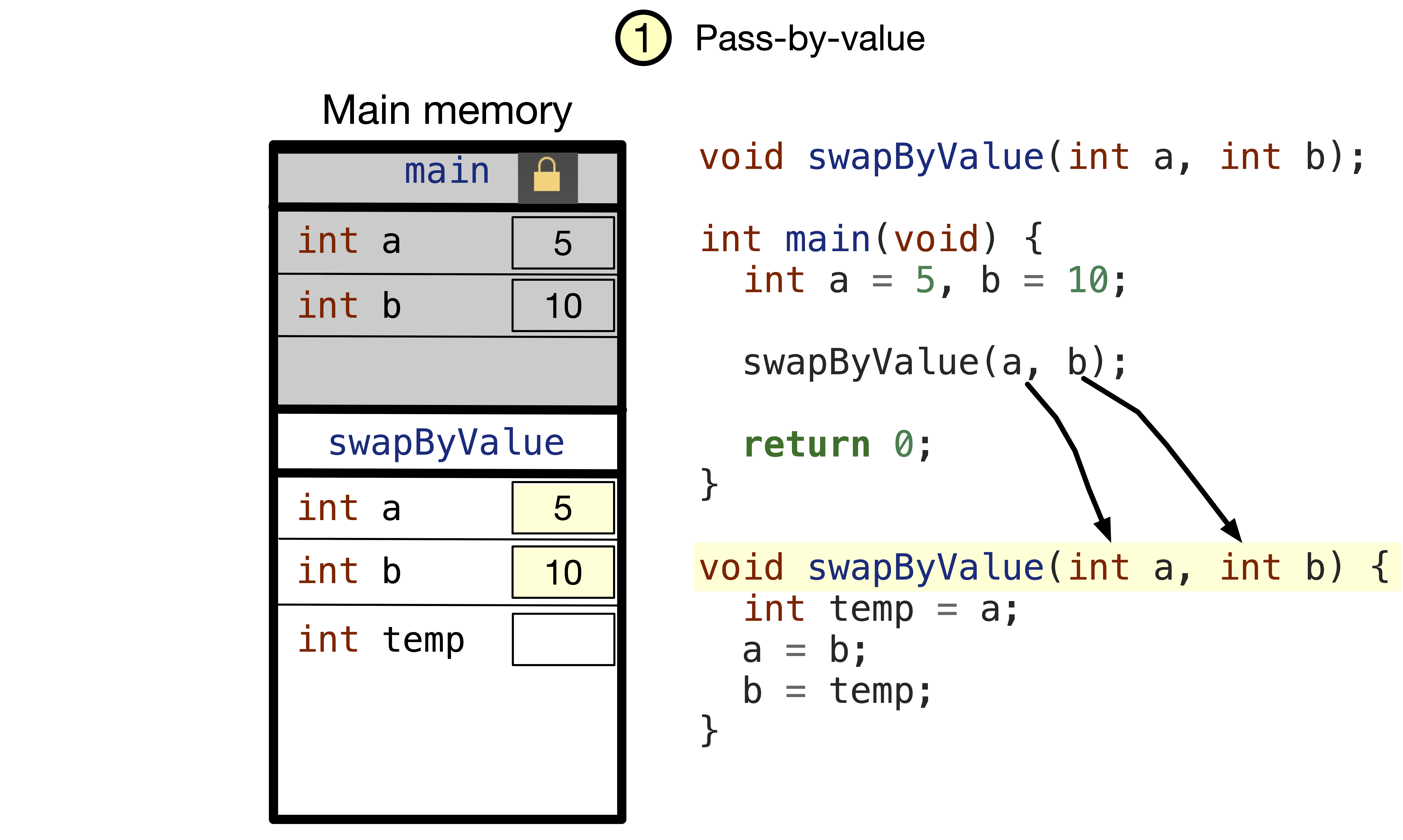
Pass by value — Fig. 1.6 `a` and `b` are passed by value to the `swapByValue` function.#

Swap local variables — Fig. 1.7 Swap the local variables `a` and `b` in the `swapByValue` function.#

Return to main function — Fig. 1.8 After returning to the `main` function, the values of `a` and `b` remain unchanged as changes happened in the local variables in the `swapByValue` frame.#

In short, we cannot use pass-by-value when we expect the changes made to the input parameters to be reflected in the main function. Instead, we can use either pass-by-reference or pass-by-pointer.

1.4.1.1. Pass-By-Pointer#

We want to ensure variables in the calling function are changed in the caller function. Instead of passing the values of the variables, we need to pass the addresses of the variables. This way, the function can access the memory locations of the variables and change their values directly. This is known as pass-by-pointer.

Back to the swapping problem, instead of passing the values of a and b to the swapByValue function, we need to pass the address of a and b to the function. The function will then swap the values of a and b using the addresses of a and b.

Pointers Recap

To pass the address of a variable to a function, you must use a pointer. A pointer is a variable that stores the memory address of another variable.

A pointer is declared by adding an asterisk * after the data type. For example, to declare a pointer to an integer, you would write int *ptr;. The pointer ptr can store the memory address of an integer variable.

Get an address of a variable. To get an address of a variable, you use the reference operator & before the variable name. For example, in the following code the variable ptr is storing the address of the variable a. We get the address of a by writing &a.

int a;
int* ptr = &a;

Get the value of a variable at an address. To access the value stored at the memory address stored in a pointer, you use the dereference operator * before the pointer name. For example, to access the value stored at the memory address stored in ptr, you would write *ptr.

In Fig. 1.9, we declare a pointer ptr and set it’s value to the memory address of the variable a: ptr = &a.

Then, we dereference ptr to access the value of a and change it to 10. In *ptr = 10;, *ptr is equivalent to *(&a). As we dereference the address of a, we can change the value of a to 10.

Then, in b = *ptr we change the value of b to a. We access a through *ptr and assign it to b by writing b = *ptr. This is equivalent to b = a.

The following code fixes the swap function to ensure the values of a and b are swapped using pass-by-pointer.

Code


#include <iostream>
using namespace std;


void swapByPointers(int* pa, int* pb);


int main(void) {
  int a = 5, b = 10;
  cout << "Before swapping: " << "a = " << a << ", b = " << b << endl;
  swapByPointers(&a, &b);
  cout << "After swapping: " << "a = " << a << ", b = " << b << endl;
  return 0;
}


void swapByPointers(int* pa, int* pb) {
  int temp = *pa;
  *pa = *pb;
  *pb = temp;
}

[Line 4] To pass the addresses of integers a and b to the swap function, we need to change the function prototype to accept pointers to integers. The function signature should be void swapByPointers(int* pa, int* pb);. The * operator is used after the data type to declare a pointer to an integer.

[Line 9] When the function is called, we pass the address of a and b by calling the function swapByPointers(&a, &b);. The & operator is used before a and b to get their addresses.

[Line 14] The function then receives the address of a into pa and the address of b into pb.

[Line 15 to 17] In the function, we dereference the pointer pa to get access to a and pb to get access to b in the main function. We then swap the values of a and b by assigning *pb to *pa and *pa to *pb.

Pass by pointer — Fig. 1.10 `a` and `b` are passed by pointer to the `swapByPointers` function.#

addresses of a and b are used to swap — Fig. 1.11 The addresses of `a` and `b` are used to change their values in the main function. `a` is accessed by dereferencing `pa` and `b` is accessed by dereferencing `pb`.#

Return from main function after swap by pointers — Fig. 1.12 When the `a` and `b` are swapped in the `swapByPointers` function, the changes are reflected in the `main` function.#

1.4.1.2. Pass-By-Reference#

Pass-by-pointer can be error prone and complex as the programmer has to take care of the syntax of * and & operators. To simplify the process, C++ provides a feature called pass-by-reference.

What is a reference? In C++, a reference is an alias, an alternate identifier/name, for another variable. For example, in the following code, a is an integer. We create a reference to a by writing int& ra = a;, where the type of ra is int&. Any changes made to ra will affect a and vice versa.

int a = 5;
int& ra = a;

In the following code example, ra is a reference to the variable a. We use ra to change the value of a to 10. The value of a is then printed to the console.

Then, we use ra to change the value of a to b. Note that ra = b does not reassign ra to refer to b. Once ra was declared to refer to a, it will never refer to any other variable.

Code


#include <iostream>
using namespace std;


int main(void) {
  int a = 5, b = 12;
  int& ra = a; // ra is a reference to a
  cout << "Point 1: ra = " << ra << ", a = " << a << endl; 

  ra = 10; // changes the value of a to 10
  cout << "Point 2: ra = " << ra << ", a = " << a << endl; 

  ra = b; // changes the value of a to b
  cout << "Point 3: ra = " << ra << ", a = " << a << endl;  
  return 0;
}

A few important notes on references:

A reference must be initialized when it is declared. For example, we cannot do int& ra; as we must declare and initialize ra at the same time.
A reference cannot be reassigned to another variable. Once a reference is assigned to a variable, it cannot be reassigned to another variable. For example, int& ra = a; means ra is a reference to a. We cannot change ra to be a reference to another variable b.
A reference is not a separate variable. It does not have a separate memory location. It is only an alias to another variable.
Don’t confuse references with pointers. References are not pointers. They are aliases to variables. The operators * and & are not used with references. The type of a reference is the same as the type of the variable it refers to. We only add & after the type to declare a reference.

How can we use references to avoid the syntax-heavy pass-by-pointers? To functions, we can pass references to variables and change the values of variables. For example, in the swap function, instead of passing the addresses of a and b, we can pass references to a and b.

Code


#include <iostream>
using namespace std;


void swapByRef(int& ra, int& rb);


int main(void) {
  int a = 5, b = 10;
  cout << "Before swapping: " << "a = " << a << ", b = " << b << endl;
  swapByRef(a, b);
  cout << "After swapping: " << "a = " << a << ", b = " << b << endl;
  return 0;
}


void swapByRef(int& ra, int& rb) {
  int temp = ra;
  ra = rb;
  rb = temp;
}

[Line 4] We change the function prototype to accept references to integers. The function signature should be void swapByValue(int& ra, int& rb);. The & operator is used after the data type to declare a reference to an integer.

[Line 9] When the function is called, we pass a and b to set the reference ra to a and rb to b.

[Line 14 to 17] The function then sets the reference ra to a and rb to b. In the function, ra and rb are used to access the values of a and b in the main function. We then swap the values of a and b by assigning ra to rb and rb to ra.

1.4.2. Reference vs. Pointer#

References and pointers maybe confused with each other as they both allow you to access the memory address of a variable. However, there are some key differences between references and pointers:

Reference is safer than a pointer. A reference cannot be NULL and must be initialized when declared. A pointer can be NULL and can point to any memory location. Dereferencing a NULL pointer can cause a segmentation fault.
References do not have separate memory locations. They are aliases to variables. Pointers have separate memory locations and store the memory address of another variable.
A reference cannot be reassigned to another variable. Once a reference is assigned to a variable, it cannot be reassigned to another variable. A pointer can be reassigned to another memory location.

This concludes our discussion on functions and methods of passing input parameters to functions. In the next section, we will discuss how should we distribute our functions into multiple files to help the compiler in generating the “executable” file.

Khufu: Object-Oriented Programming using C++

Passing Input Parameters to Functions

Contents

1.4. Passing Input Parameters to Functions#

1.4.1. Problem with Pass-By-Value#

1.4.1.1. Pass-By-Pointer#

1.4.1.2. Pass-By-Reference#

1.4.2. Reference vs. Pointer#